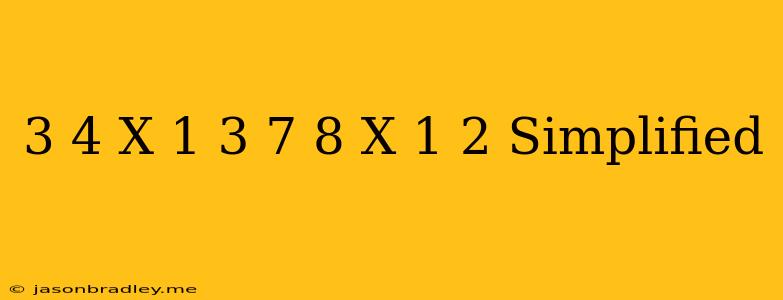Simplifying the Expression: 3/4x - 1/3 + 7/8x - 1/2
This article will guide you through the process of simplifying the algebraic expression: 3/4x - 1/3 + 7/8x - 1/2.
1. Combine Like Terms
First, we need to identify the like terms in the expression. Like terms have the same variable and exponent. In this case, we have two terms with "x": 3/4x and 7/8x. We also have two constant terms: -1/3 and -1/2.
Let's combine the "x" terms:
- 3/4x + 7/8x
To add fractions, they must have a common denominator. The least common denominator for 4 and 8 is 8.
- (3/4 * 2/2)x + 7/8x = 6/8x + 7/8x = 13/8x
Now, let's combine the constant terms:
- -1/3 - 1/2
Again, we need a common denominator. The least common denominator for 3 and 2 is 6.
- (-1/3 * 2/2) - (1/2 * 3/3) = -2/6 - 3/6 = -5/6
2. Combine the Simplified Terms
Now we have two simplified terms: 13/8x and -5/6. Putting them together, the simplified expression is:
13/8x - 5/6
Conclusion
By combining like terms, we have simplified the expression 3/4x - 1/3 + 7/8x - 1/2 into 13/8x - 5/6. This is the simplest form of the expression, as the terms cannot be further combined.