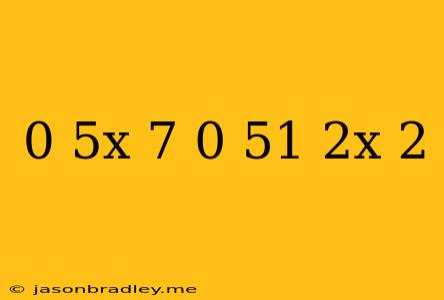Solving the Exponential Equation: 0.5^x + 7 * 0.5^(1-2x) = 2
This article will guide you through the steps of solving the exponential equation 0.5^x + 7 * 0.5^(1-2x) = 2.
Simplifying the Equation
-
Rewrite 0.5 as (1/2):
The equation becomes: (1/2)^x + 7 * (1/2)^(1-2x) = 2 -
Use the property of exponents a^(m-n) = a^m / a^n: (1/2)^x + 7 * (1/2)^1 / (1/2)^2x = 2
-
Simplify: (1/2)^x + 7 * (1/2) / (1/2)^2x = 2
-
Combine terms with the same base: (1/2)^x + 7 * (1/2)^(1-2x) = 2 (1/2)^x + 7 * (1/2)^(1-2x) = 2 (1/2)^x + 7 * (1/2)^1 * (1/2)^(-2x) = 2 (1/2)^x + 7 * (1/2) * (1/2)^(-2x) = 2 (1/2)^x + 7/2 * (1/2)^(-2x) = 2
Solving for x
-
Make a substitution: Let y = (1/2)^x.
The equation becomes: y + 7/2 * y^(-2) = 2 -
Multiply both sides by y^2: y^3 + 7/2 = 2y^2
-
Rearrange into a cubic equation: y^3 - 2y^2 + 7/2 = 0
-
Solve for y: You can use various methods to solve this cubic equation, such as the Rational Root Theorem, factoring, or numerical methods. This step might require a calculator or specialized software.
-
Substitute back for x:
Once you find the values of y, substitute them back into y = (1/2)^x and solve for x. Remember to check if the solutions are valid by plugging them back into the original equation.
Conclusion
Solving this exponential equation requires careful manipulation of exponents and the use of appropriate techniques to solve the resulting cubic equation. Remember to check your solutions to ensure they are valid.