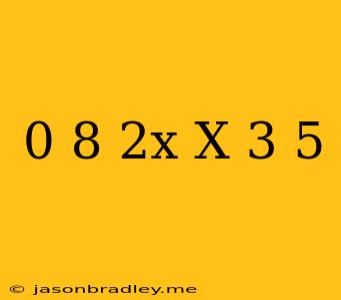Solving the Equation: 0.8 + 2x = x + 3.5
This article will guide you through the steps to solve the linear equation 0.8 + 2x = x + 3.5.
Step 1: Simplify both sides
First, we can simplify both sides of the equation by combining like terms. On the left side, there are no like terms to combine. However, on the right side, we can subtract 'x' from both sides to get all the 'x' terms on one side:
0.8 + 2x - x = x + 3.5 - x
0.8 + x = 3.5
Step 2: Isolate the 'x' term
To isolate the 'x' term, we need to get rid of the constant term (0.8) on the left side. We can do this by subtracting 0.8 from both sides:
0.8 + x - 0.8 = 3.5 - 0.8
x = 2.7
Step 3: Solution
The solution to the equation 0.8 + 2x = x + 3.5 is x = 2.7. This means that if we substitute 'x' with 2.7 in the original equation, the equation will be true.
Verification
To verify the solution, we can plug 'x = 2.7' back into the original equation:
0.8 + 2(2.7) = 2.7 + 3.5
0.8 + 5.4 = 6.2
6.2 = 6.2
This shows that the solution is correct, as both sides of the equation are equal.