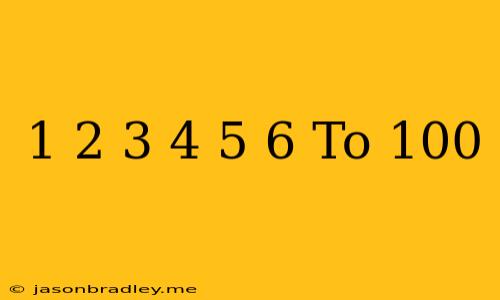The Sum of the First 100 Natural Numbers
The sum of the first 100 natural numbers, represented as 1 + 2 + 3 + 4 + 5 + 6... + 100, is a classic mathematical problem with a simple and elegant solution.
Understanding the Pattern
Instead of adding each number individually, there's a clever way to visualize the sum:
- Pair the numbers: Pair the first and last number (1 + 100), the second and second-to-last (2 + 99), and so on.
- Equal sums: Notice that each pair adds up to the same value (101).
- Number of pairs: Since we have 100 numbers, we have 50 pairs.
The Formula
This leads to the formula:
(Sum of first 100 natural numbers) = (Number of pairs) * (Sum of each pair)
Therefore, the sum is: 50 * 101 = 5050
Generalizing the Solution
This method can be generalized for any sequence of consecutive natural numbers. The sum of the first 'n' natural numbers is:
(n/2) * (n + 1)
For example, to find the sum of the first 20 natural numbers:
(20/2) * (20 + 1) = 10 * 21 = 210
Conclusion
The sum of the first 100 natural numbers is 5050. This simple formula and the visualization of pairing numbers provide a clear and efficient way to calculate this sum, and it can be applied to any sequence of consecutive natural numbers.