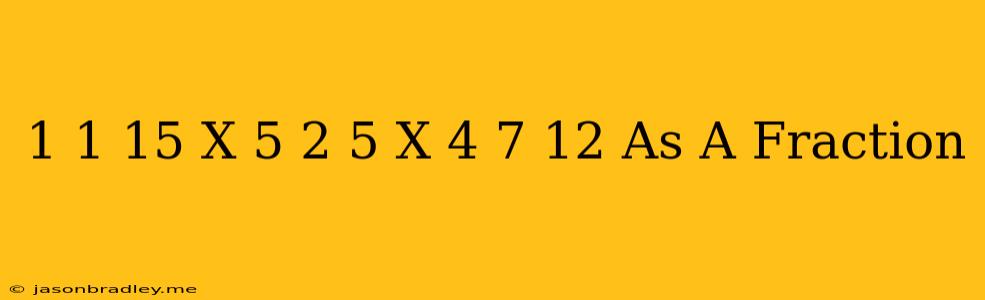Multiplying Mixed Numbers: A Step-by-Step Guide
This article will guide you through the process of multiplying mixed numbers, specifically focusing on the example of 1 1/15 x 5 2/5 x 4 7/12.
Converting Mixed Numbers to Improper Fractions
The first step is to convert each mixed number into an improper fraction. Remember that a mixed number represents a whole number plus a fraction.
Here's how to convert each mixed number:
- 1 1/15: Multiply the whole number (1) by the denominator (15) and add the numerator (1). Keep the same denominator (15). This gives us 16/15.
- 5 2/5: Multiply the whole number (5) by the denominator (5) and add the numerator (2). Keep the same denominator (5). This gives us 27/5.
- 4 7/12: Multiply the whole number (4) by the denominator (12) and add the numerator (7). Keep the same denominator (12). This gives us 55/12.
Now our problem looks like this: 16/15 x 27/5 x 55/12
Multiplying Fractions
To multiply fractions, we simply multiply the numerators and the denominators.
(16 x 27 x 55) / (15 x 5 x 12)
Simplifying the Fractions
Before performing the multiplication, let's simplify the fractions by finding common factors in the numerators and denominators.
- 16/15 cannot be simplified further.
- 27/5 cannot be simplified further.
- 55/12 cannot be simplified further.
However, we can notice that 12 and 55 both share a common factor of 4. We can simplify the fraction 55/12 by dividing both numerator and denominator by 4, resulting in 11/3.
Now our problem looks like this: 16/15 x 27/5 x 11/3
Performing the Multiplication
Now, we can multiply the numerators and the denominators:
(16 x 27 x 11) / (15 x 5 x 3)
This gives us 4752 / 225
Simplifying the Result
Finally, we can simplify the improper fraction by dividing both numerator and denominator by their greatest common factor, which is 9.
4752 / 225 = 528 / 25
Therefore, 1 1/15 x 5 2/5 x 4 7/12 = 528/25.