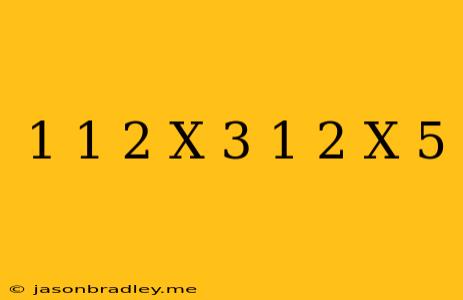Let's Explore the World of Mixed Numbers: 1 1/2 x 3 1/2 x 5
In the realm of mathematics, mixed numbers offer a unique way to represent fractions. Today, we'll delve into the multiplication of three mixed numbers: 1 1/2 x 3 1/2 x 5.
Understanding Mixed Numbers
Before diving into the multiplication, let's understand what mixed numbers represent. A mixed number combines a whole number with a fraction. For example, 1 1/2 represents one whole unit plus one-half.
Converting Mixed Numbers to Fractions
To multiply mixed numbers, it's easier to convert them into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
- 1 1/2: Multiply the whole number (1) by the denominator (2) and add the numerator (1): 1 x 2 + 1 = 3. Keep the same denominator (2). Therefore, 1 1/2 = 3/2.
- 3 1/2: Multiply the whole number (3) by the denominator (2) and add the numerator (1): 3 x 2 + 1 = 7. Keep the same denominator (2). Therefore, 3 1/2 = 7/2.
Multiplication of Fractions
Now we have the equation: 3/2 x 7/2 x 5/1. To multiply fractions, simply multiply the numerators and the denominators:
- Numerator: 3 x 7 x 5 = 105
- Denominator: 2 x 2 x 1 = 4
This results in 105/4.
Converting Back to a Mixed Number
The final step is to convert the improper fraction back to a mixed number. Divide the numerator (105) by the denominator (4).
- 105 divided by 4 is 26 with a remainder of 1.
- The whole number part of the mixed number is 26.
- The fraction part is the remainder (1) over the original denominator (4): 1/4
Therefore, 1 1/2 x 3 1/2 x 5 = 26 1/4.
Conclusion
By converting mixed numbers to fractions and applying the rules of fraction multiplication, we successfully multiplied 1 1/2 x 3 1/2 x 5 and obtained the result 26 1/4. This journey highlights the power of understanding different mathematical representations and applying appropriate techniques for solving complex problems.