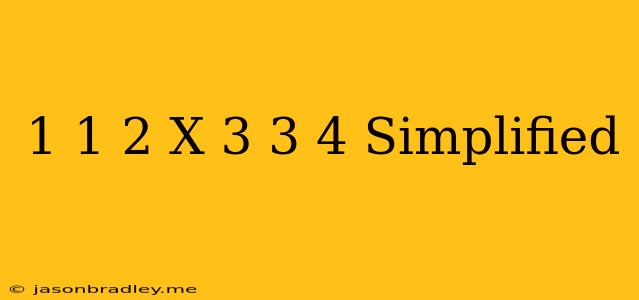Simplifying Mixed Numbers: 1 1/2 x 3 3/4
Multiplying mixed numbers might seem daunting, but it's actually quite simple with the right approach. Let's break down how to simplify the expression 1 1/2 x 3 3/4.
Converting to Improper Fractions
The first step is to convert both mixed numbers into improper fractions. Remember, an improper fraction has a numerator larger than its denominator.
-
1 1/2: To convert this, multiply the whole number (1) by the denominator (2) and add the numerator (1). Keep the same denominator. This gives us (1 * 2 + 1)/2 = 3/2.
-
3 3/4: Following the same process, we get (3 * 4 + 3)/4 = 15/4.
Multiplying the Fractions
Now we have a simple multiplication problem: (3/2) x (15/4).
To multiply fractions, we multiply the numerators and the denominators.
- (3 x 15) / (2 x 4) = 45/8
Simplifying the Result
The final step is to simplify the improper fraction 45/8. We can do this by dividing the numerator by the denominator:
- 45 ÷ 8 = 5 with a remainder of 5
This means 45/8 is equal to 5 5/8.
Conclusion
Therefore, 1 1/2 x 3 3/4 simplified is 5 5/8. By converting mixed numbers to improper fractions and then multiplying, we can easily solve this kind of problem.