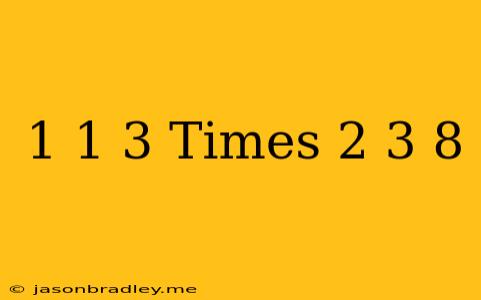Multiplying Mixed Numbers: 1 1/3 x 2 3/8
This article will guide you through the process of multiplying mixed numbers, using the example of 1 1/3 x 2 3/8.
1. Convert Mixed Numbers to Improper Fractions
The first step is to convert both mixed numbers into improper fractions. Here's how:
- 1 1/3: Multiply the whole number (1) by the denominator (3) and add the numerator (1). Keep the same denominator. (1 x 3 + 1) / 3 = 4/3
- 2 3/8: Multiply the whole number (2) by the denominator (8) and add the numerator (3). Keep the same denominator. (2 x 8 + 3) / 8 = 19/8
Now our problem is: 4/3 x 19/8
2. Multiply the Numerators and Denominators
Multiply the numerators together and the denominators together:
(4 x 19) / (3 x 8) = 76/24
3. Simplify the Result
The fraction 76/24 can be simplified. Find the greatest common factor (GCF) of 76 and 24, which is 4. Divide both the numerator and denominator by 4:
76/4 = 19 24/4 = 6
Therefore, the simplified answer is 19/6.
4. Convert Back to a Mixed Number (Optional)
If you need the answer in mixed number form, divide the numerator (19) by the denominator (6):
19 ÷ 6 = 3 with a remainder of 1
This means the mixed number is 3 1/6.
Conclusion
By following these steps, you can confidently multiply any two mixed numbers. Remember to always simplify your answer whenever possible.