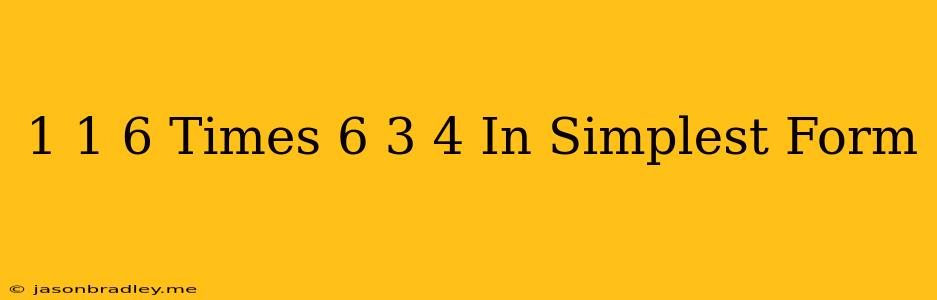Multiplying Mixed Numbers: 1 1/6 x 6 3/4
This article will guide you through the steps of multiplying the mixed numbers 1 1/6 and 6 3/4 and expressing the answer in its simplest form.
Converting Mixed Numbers to Improper Fractions
The first step is to convert both mixed numbers into improper fractions. To do this, we follow these steps:
-
Multiply the whole number by the denominator of the fraction:
- For 1 1/6: 1 x 6 = 6
- For 6 3/4: 6 x 4 = 24
-
Add the numerator of the fraction to the result:
- For 1 1/6: 6 + 1 = 7
- For 6 3/4: 24 + 3 = 27
-
Keep the original denominator:
- For 1 1/6: 7/6
- For 6 3/4: 27/4
Now we have the following improper fractions: 7/6 and 27/4.
Multiplying the Fractions
To multiply fractions, we simply multiply the numerators and the denominators:
(7/6) x (27/4) = (7 x 27) / (6 x 4) = 189/24
Simplifying the Result
The fraction 189/24 can be simplified by finding the greatest common factor (GCF) of 189 and 24. The GCF is 3. Dividing both numerator and denominator by 3, we get:
189/24 = (189/3) / (24/3) = 63/8
Converting Back to a Mixed Number
Finally, we can convert the improper fraction 63/8 back to a mixed number:
- Divide the numerator by the denominator: 63 / 8 = 7 with a remainder of 7.
- The quotient (7) becomes the whole number part.
- The remainder (7) becomes the numerator of the fraction.
- Keep the original denominator (8).
Therefore, the simplest form of the product of 1 1/6 and 6 3/4 is 7 7/8.