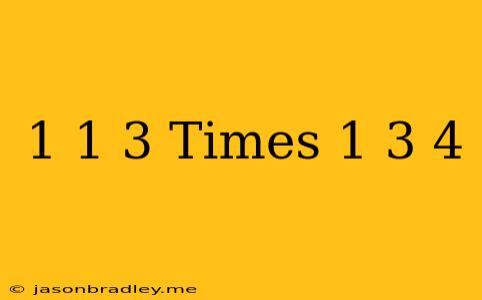Multiplying Mixed Numbers: 1 1/3 x 1 3/4
This article will walk you through the steps of multiplying the mixed numbers 1 1/3 and 1 3/4.
Converting Mixed Numbers to Fractions
Before multiplying, we need to convert the mixed numbers into improper fractions. Here's how:
- 1 1/3: Multiply the whole number (1) by the denominator (3) and add the numerator (1). Keep the same denominator. This gives us (1 * 3 + 1)/3 = 4/3.
- 1 3/4: Multiply the whole number (1) by the denominator (4) and add the numerator (3). Keep the same denominator. This gives us (1 * 4 + 3)/4 = 7/4.
Multiplying Fractions
Now that we have improper fractions, we can multiply them:
(4/3) * (7/4) = (4 * 7) / (3 * 4) = 28/12
Simplifying the Result
The fraction 28/12 can be simplified. We can divide both the numerator and denominator by their greatest common factor, which is 4:
28/12 = (28/4) / (12/4) = 7/3
Converting Back to a Mixed Number (Optional)
The result, 7/3, is an improper fraction. If you want to express it as a mixed number, divide the numerator (7) by the denominator (3):
7 ÷ 3 = 2 with a remainder of 1.
This means that 7/3 is equivalent to 2 1/3.
Therefore:
1 1/3 * 1 3/4 = 7/3 or 2 1/3