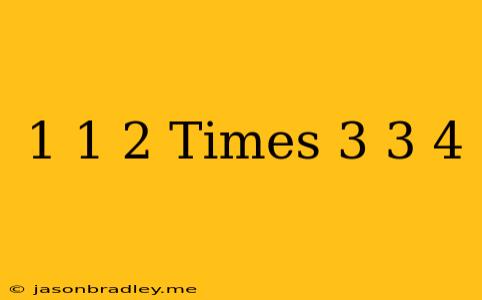Multiplying Mixed Numbers: 1 1/2 x 3 3/4
This article will guide you through the process of multiplying the mixed numbers 1 1/2 and 3 3/4.
Understanding Mixed Numbers
Before we start, let's review what mixed numbers are. A mixed number combines a whole number and a fraction. For example, 1 1/2 represents one whole and one half.
Converting to Improper Fractions
To multiply mixed numbers, it's easiest to first convert them into improper fractions. To do this:
- Multiply the whole number by the denominator of the fraction:
- 1 x 2 = 2
- 3 x 4 = 12
- Add the numerator to the product:
- 2 + 1 = 3
- 12 + 3 = 15
- Keep the same denominator:
- 1 1/2 becomes 3/2
- 3 3/4 becomes 15/4
Multiplying Improper Fractions
Now that we have improper fractions, we can multiply them:
- Multiply the numerators: 3 x 15 = 45
- Multiply the denominators: 2 x 4 = 8
- Simplify the result: 45/8
Converting Back to a Mixed Number
The improper fraction 45/8 can be converted back to a mixed number:
- Divide the numerator by the denominator: 45 ÷ 8 = 5 with a remainder of 5
- The quotient (5) becomes the whole number part of the mixed number.
- The remainder (5) becomes the numerator of the fraction.
- Keep the same denominator (8).
Therefore, 45/8 is equal to 5 5/8.
Conclusion
By converting mixed numbers into improper fractions, multiplying, and then converting back, we have found that 1 1/2 x 3 3/4 = 5 5/8. Remember this process for future multiplications of mixed numbers.