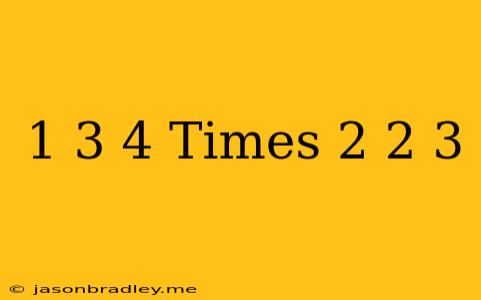Multiplying Mixed Numbers: 1 3/4 x 2 2/3
This article will guide you through multiplying the mixed numbers 1 3/4 and 2 2/3.
Converting Mixed Numbers to Improper Fractions
Before multiplying mixed numbers, we need to convert them to improper fractions. Here's how:
1. Multiply the whole number by the denominator:
- For 1 3/4: 1 x 4 = 4
- For 2 2/3: 2 x 3 = 6
2. Add the numerator to the result:
- For 1 3/4: 4 + 3 = 7
- For 2 2/3: 6 + 2 = 8
3. Keep the same denominator:
- 1 3/4 becomes 7/4
- 2 2/3 becomes 8/3
Multiplying Improper Fractions
Now that we have improper fractions, we can multiply them:
(7/4) x (8/3)
To multiply fractions, we simply multiply the numerators and the denominators:
(7 x 8) / (4 x 3)
This simplifies to:
56/12
Simplifying the Answer
The improper fraction 56/12 can be simplified. We can find the greatest common factor (GCF) of 56 and 12, which is 4. Dividing both numerator and denominator by 4, we get:
14/3
Converting Back to Mixed Number
Finally, we can convert the improper fraction 14/3 back to a mixed number:
- Divide the numerator (14) by the denominator (3): 14 ÷ 3 = 4 with a remainder of 2.
- The quotient (4) becomes the whole number part: 4
- The remainder (2) becomes the numerator of the fraction: 2
- Keep the same denominator: 3
Therefore, 1 3/4 x 2 2/3 = 4 2/3.