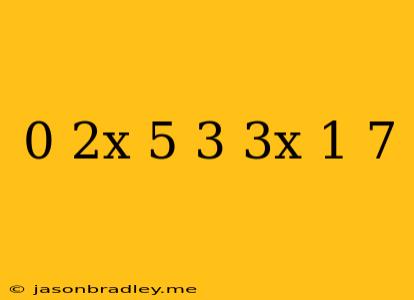Solving the Equation: 0.2x + 5/3 = 3x - 1/7
This article will guide you through the steps of solving the linear equation 0.2x + 5/3 = 3x - 1/7.
Step 1: Eliminate Fractions
The first step is to get rid of the fractions by multiplying both sides of the equation by the least common multiple (LCM) of the denominators (3 and 7). The LCM of 3 and 7 is 21.
21 * (0.2x + 5/3) = 21 * (3x - 1/7)
This simplifies to:
4.2x + 35 = 63x - 3
Step 2: Combine Like Terms
Next, we need to isolate the x terms on one side of the equation and the constant terms on the other. Subtract 4.2x from both sides and add 3 to both sides:
35 + 3 = 63x - 4.2x
This simplifies to:
38 = 58.8x
Step 3: Isolate x
Finally, divide both sides by 58.8 to isolate x:
x = 38 / 58.8
Step 4: Simplify the Solution
Simplify the solution by dividing both numerator and denominator by their greatest common factor (2):
x = 19 / 29.4
This can be further simplified by multiplying both numerator and denominator by 10:
x = 190 / 294
Solution
Therefore, the solution to the equation 0.2x + 5/3 = 3x - 1/7 is x = 190/294. You can further simplify this fraction by finding the greatest common factor of 190 and 294, which is 2. This gives you a simplified solution of x = 95/147.